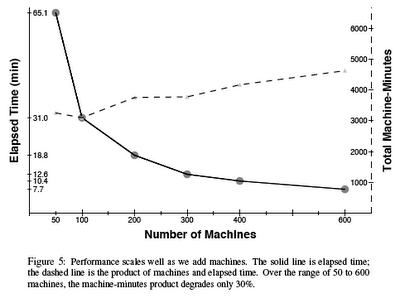
"The set of aggregations is limited but the query phase can involve more general computations, which we express in a new interpreted, procedural programming language called Sawzall†"More important, for our purposes, is Section 12 Performance. It includes the following plot, which tells us something about Sawzall scalability; but not everything.† Not related to the portable reciprocating power saw manufactured by the Milwaukee Electric Tool Corporation.
What struck me about the elapsed time in the lower curve (joined dots) is how much it resembles the lowest (dotted) curve in Figure 9.19 of my Perl::PDQ book:
There, I use PDQ to analyze the parallel query performance of what is currently known as the NCR/Teradata WorldMark massively parallel data-warehouse product. It is a distributed architecture involving both front-end processors (FEPs) and back-end processors (BEPs). The back-ends are SMPs with the database tables striped across the SMP local disks.
In Figure 9.19 you see the primary effect of throwing massive parallelism at a DSS query. The lowest (dotted) curve represents the query execution time R(p) as a function of the number of BEPs (p). The query time decreases rapidly toward the x-axis as more parallel BEPs are configured with the DB tables re-striped (naturally).
The question I address in my book is: What is the optimal number of BEPs? Should I quit reconfiguring BEPs (a non-trivial, not to mention potentially expensive task, BTW) at p = 10, 20, ... ? In other words, where is the point of diminishing returns? I know precisely how to do that for the case of throughput scalability—that's what my Universal Scalability Law (USL) is all about—but here we're considering response time, not throughput! That's where PDQ comes in.
While applying PDQ to the WorldMark data (many moons ago), I discovered something very interesting. PDQ not only computes response time and throughput for each BEP configuration, but also the saturation throughput (the uppermost curve in Fig. 19.9). Looking at that curve, it's very clear the saturation throughput develops a knee, which turns out to be at p = 90 BEPs, and that corresponds exactly to the optimal BEP configuration as measured on the real machine. There's a good reason for that, which means this observation can be expressed as a completely general rule:
The saturation throughput is actually comprised of two curves: a horizontal line and a diagonal line. The knee occurs where the diagonal line intersects the horizontal line. The optimal configuration is determined by dropping an imaginary vertical line down onto the x-axis and reading off the number of BEPs.Applying this rule to Figure 9.19, we get p = 90. I will discuss this rule in more detail in my Guerrilla Capacity Planning class, next week.
This plot was produced using PDQ-R and, although it matches Fig. 5 (above) from the Google paper, it includes some new information. In particular, the blue dashed curve does not appear in the Google plot because it is the theoretical response-time curve computed by PDQ. You can see that it matches the Elapsed Time data (circles) quite well without trying to do anything fancy.
The measured capacity-time data (boxes) are also included with their mean value shown as the horizontal dotted line. That line can be compared with the theoretical value (dashed horizontal line) computed by PDQ. The corresponding units for the capacity-time product are shown on the right-hand y-axis. I'll come back to the significance of these data, shortly. Here's the R code that did the job:
# sawzall.r
# Created by NJG on Tuesday, November 10, 2009
library(pdq)
# Google data
sawzrtdata <- matrix(c(50, 100, 200, 300, 400, 600, 65.1, 31.0, 18.8, 12.6, 10.4, 7.7),nrow=6,ncol=2)
sawzmtdata <- matrix(c(50, 100, 200, 300, 400, 600, 65.1*50, 31.0*100, 18.8*200, 12.6*300, 10.4*400, 7.7*600),nrow=6,ncol=2)
servtime <- min(sawzmtdata[,2]) # 3100 minutes
arrivrate <- 0.000010
workname <- "file"
machines <- 650
plotsteps <- 10
paraname<-1:machines
rt <- 1:machines # residence time at machine
mt <- 1:machines # machine-time product (should be constant)
xc <- 1:machines # number of machines to plot on x-axis
rx <- 0:machines
ry <- 0:machines
my <- 0:machines
for (k in 1:machines) {
Init("sawzpdq")
CreateOpen(workname, arrivrate)
for(m in 1:k) {
paraname[m]<-sprintf("mach%d", m)
CreateNode(paraname[m], CEN, FCFS)
SetDemand(paraname[m], workname, servtime/k)
}
Solve(CANON)
xc[k] <- k
rt[k] <- GetResponse(TRANS, workname) / k
mt[k] <- k * rt[k]
if (k==1) {
u1 <- GetUtilization(paraname[k], workname, TRANS)
q1 <- GetQueueLength(paraname[k], workname, TRANS)
}
if (k==600) {
u600 <- GetUtilization(paraname[k], workname, TRANS)
q600 <- GetQueueLength(paraname[k], workname, TRANS)
}
}
# mod the data above 40 (to include 50) for plotting
rx <- which(xc %% plotsteps == 0 & xc > 30, arr.ind = TRUE)
ry <- rt[rx]
my <- mt[rx]
plot(rx,ry,main="PDQ Model of Sawzall",xlab="Number of Machines, p",
ylab="Elapsed Time, T(p)",type="l",bty="c",col="blue",xlim=c(40,650),ylim=c(0,80))
points(sawzrtdata)
lines(rx, servtime/rx, lty="dashed",lwd=2)
# Capacity-time line
par(new=TRUE)
plot(rx,my,ylim=c(1000,6000),type="l",lty="dashed",
bty="c",xlab="",ylab="",axes=FALSE)
axis(side=4,line=-1)
mtext("(p x T)",side=4)
points(sawzmtdata,type="b",pch=22)
abline(h=mean(sawzmtdata[,2]),lty="dotted") # hyperbolic curve
# Summary metrics
cat(sprintf("Xmax: %10.8f\n", arrivrate))
cat(sprintf("U[001]: %10.8f, Q[001]: %6.4f\n", u1, q1))
cat(sprintf("U[600]: %10.8f, Q[600]: %6.4f\n", u600, q600))
# Check utilization of random machines
cat(sprintf("Number of machines: %3d\n", machines))
for (i in 1:2) {
rm <- round(runif(1,1,machines))
ru <- GetUtilization(paraname[rm], workname, TRANS)
cat(sprintf("U[%03d]: %10.8f\n", rm, ru))
}
The elapsed time T(1) on a single machine is taken to be the minimum of the capacity-time product. We use T(1) as the service time in the PDQ model. We can believe that number because the PDQ fit to the Google elapsed-time data is so good. The complete curve corresponds to successive parallel PDQ nodes in parallel. The way to do that is described in my previous post about parallelism in PDQ, which you can compare with the above PDQ-R code.
Since Sawzall is executing a form of batch processing, we set things up in PDQ so that the amount of mean queueing (waiting) is very small. The last few lines of the PDQ-R code help us to check that:
Xmax: 0.00001000
U[001]: 0.03100000, Q[001]: 0.0320
U[600]: 0.00005167, Q[600]: 0.0001
Number of machines: 650
U[623]: 0.00004769
U[171]: 0.00004769
Returning now to the Google capacity-time data (squares), although those data cannot help you determine the optimal machine configuration, they are useful measure of parallel performance. Here's how it works.
The main objective of Sawzall, Hadoop and MapReduce, etc., is to reduce the elapsed time $T(1)$ by throwing more machines at it, i.e., increasing $p$. Assuming the workload can be repartitioned, the reduction in time must follow:
\begin{equation} T(p) = \dfrac{T(1)}{p} \end{equation}
which is a hyperbolic function in $p$ and that's precisely the kind of profile we see in both the Google data (circles) and my PDQ-R model (blue curve).
By the same token, multiplying both sides of eqn. (1) by p produces:
\begin{equation} p ~T(p) = T(1) \end{equation}
Since $T(1)$ has the same value independent of the configuration p, the machine-time product in eqn. (2) should be constant. The theoretical constant value is represented by the horizontal dashed line in my PDQ-R plot. You can see that the actual Google measurements deviate from that theoretical line and are tending to increase. That trend also matches how the elapsed-time data points sit above the (blue) PDQ curve.
In the meantime, there have also been some more recent publications regarding MR performance, which might be of interest, viz., a UCB paper: "MapReduce Online" along with more details at a UC Berkeley blog, commentaries from a Yale blog, and an O'Reilly blog. I haven't had time to peruse them yet. If you see anything else I should know about, let me know. Similarly, if you know of other benchmark data for Hadoop or MR that might benefit from the type of analysis I've done here, let me know about that also.
Update: See my follow-on post GCaP class: Sawzall Optimum, which includes new information from a former Googler—now a Guerrilla alumnus.


No comments:
Post a Comment